2.2 线性表的顺序表示
2.2.1 顺序表的定义
【命题追踪】 (算法题) 顺序表的应用 (2010、2011、2018、2020)
线性表的顺序存储又称顺序表。它是用一组地址连续的存储单元依次存储线性表中的数据元素, 从而使得逻辑上相邻的两个元素在物理位置上也相邻。第 1 个元素存储在顺序表的起始位置, 第
假设顺序表 L 存储的起始位置为 LOC (A), sizeof(ElemType) 是每个数据元素所占用存储空间的大小, 则表 L 所对应的顺序存储如图 2.1 所示。
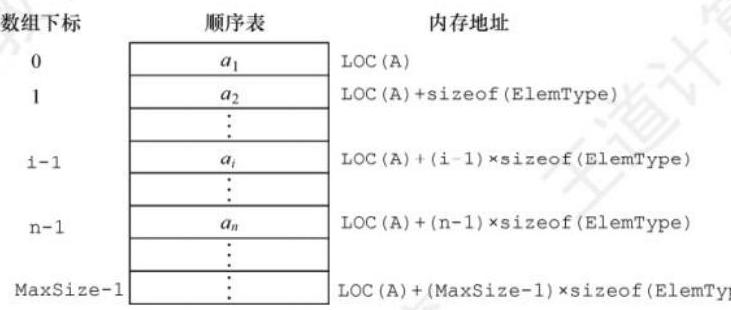
图 2.1 线性表的顺序存储结构
每个数据元素的存储位置都和顺序表的起始位置相差一个和该数据元素的位序成正比的常数, 因此, 顺序表中的任意一个数据元素都可以随机存取, 所以线性表的顺序存储结构是一种随机存取的存储结构。通常用高级程序设计语言中的数组来描述线性表的顺序存储结构。
注 意
线性表中元素的位序是从 1 开始的, 而数组中元素的下标是从 0 开始的。
假定线性表的元素类型为 ElemType, 则静态分配的顺序表存储结构描述为
//定义线性表的最大长度
#define MaxSize 50
typedef struct{
//顺序表的元素
ElemType data[MaxSize];
//顺序表的当前长度
int length;
}SqList; //顺序表的类型定义一维数组可以是 静态分配 的, 也可以是 动态分配 的。对数组进行静态分配时, 因为数组的大小和空间事先已经固定, 所以一旦空间占满, 再加入新数据就会产生溢出, 进而导致程序崩溃。
而在动态分配时, 存储数组的空间是在程序执行过程中通过动态存储分配语句分配的, 一旦数据空间占满, 就另外开辟一块更大的存储空间, 将原表中的元素全部拷贝到新空间, 从而达到扩充数组存储空间的目的, 而不需要为线性表一次性地划分所有空间。
动态分配的顺序表存储结构描述为
#define InitSize 100 //表长度的初始定义
typedef struct{
ElemType *data; //指示动态分配数组的指针
int MaxSize, length; //数组的最大容量和当前个数
}SeqList; //动态分配数组顺序表的类型定义C 的初始动态分配语句为
L.data = (ElemType*)malloc(sizeof(ElemTyle) * InitSize)C++ 的初始动态分配语句为
L.data=new ElemType[InitSize];注 意
动态分配并不是链式存储, 它同样属于顺序存储结构, 物理结构没有变化, 依然是随机存取方式, 只是分配的空间大小可以在运行时动态决定。
顺序表的主要优点:
①可进行随机访问,即可通过首地址和元素序号可以在
②存储密度高, 每个结点只存储数据元素。
顺序表的缺点也很明显:
①元素的插入和删除需要移动大量的元素,插入操作平均需要移动
②顺序存储分配需要一段连续的存储空间,不够灵活。
2.2.2 顺序表上基本操作的实现
【命题追踪】 顺序表上操作的时间复杂度分析(2023)
这里仅讨论顺序表的初始化、插入、删除和按值查找, 其他基本操作的算法都很简单。
注 意
在各种操作的实现中 (包括严蔚敏老师撰写的教材), 往往可以忽略边界条件判断、变量定义、内存分配不足等细节, 即不要求代码具有可执行性, 而重点在于算法的思想。
1. 顺序表的初始化
静态分配和动态分配的顺序表的初始化操作是不同的。静态分配在声明一个顺序表时, 就已为其分配了数组空间, 因此初始化时只需将顺序表的当前长度设为 0 。
// SqList L; //声明一个顺序表
void InitList(SqList &L) {
L.length = 0; //顺序表初始长度为 0
}动态分配的初始化为顺序表分配一个预定义大小的数组空间, 并将顺序表的当前长度设为 0 。 MaxSize 指示顺序表当前分配的存储空间大小, 一旦因插入元素而空间不足, 就进行再分配。
void InitList(SeqList &L){
L.data=(ElemType *)malloc(MaxSize*sizeof(ElemType)); //分配存储空间
L.length=0; //顺序表初始长度为 0
L.MaxSize=InitSize; //初始存储容量
}2. 插入操作
在顺序表 L 的第 i ( 1<=i<=L.length+1 ) 个位置插入新元素 e 。若 i 的输入不合法,则返回 false, 表示插入失败; 否则, 将第 i 个元素及其后的所有元素依次往后移动一个位置, 腾出一个空位置插入新元素 e ,顺序表长度增加 1,插入成功,返回 true。
bool ListInsert(SqList &L, int i, ElemType e) {
if (i<1 || i>L.length+1) { // 判断 i 的范围是否有效
return false;
}
if (L.length>=MaxSize) { // 当前存储空间已满, 不能插入
return false;
}
for(int j = L.length; j>=i; j--) { // 将第 i 个元素及之后的元素后移
L.data[j] = L.data[j-1];
}
L.data[i-1] = e; // 在位置 i 处放入 e $
L.length++; // 线性表长度加 1
return true;
}注意
区别顺序表的位序和数组下标。为何判断插入位置是否合法时 if 语句中用 length+1 , 而移动元素的 for 语句中只用 length。
最好情况: 在表尾插入 (即
最坏情况: 在表头插入 (即
平均情况: 假设
因此,顺序表插入算法的平均时间复杂度为
3. 删除操作
删除顺序表 L 中第 i ( 1<=i<=L.length+1 ) 个位置的元素,用引用变量 e 返回。若 i 的输入不合法,则返回 false; 否则,将被删元素赋给引用变量 e ,并将第 i+1 个元素及其后的所有元素依次往前移动一个位置, 返回 true。
bool ListDelete(SqList &L, int i, ElemType &e) {
if (i<1 || i>L.length) { // 判断 i 的范围是否有效
return false;
}
e = L.data[i-1]; // 将被删除的元素赋值给e
for(int j=i; j<L.length; j++) { // 将第 i 个位置后的元素前移
L.data[j-1] = L.data[j];
}
L.length--; // 线性表长度减 1
return true;
}最好情况: 删除表尾元素 (即
最坏情况: 删除表头元素 (即
平均情况: 假设
因此,顺序表删除算法的平均时间复杂度为
可见, 顺序表中插入和删除操作的时间主要耗费在移动元素上, 而移动元素的个数取决于插入和删除元素的位置。图 2.2 所示为一个顺序表在进行插入和删除操作前、后的状态, 以及其数据元素在存储空间中的位置变化和表长变化。在图 2.2(a)中,将第 4 个至第 7 个元素从后往前依次后移一个位置, 在图 2.2(b)中, 将第 5 个至第 7 个元素从前往后依次前移一个位置。
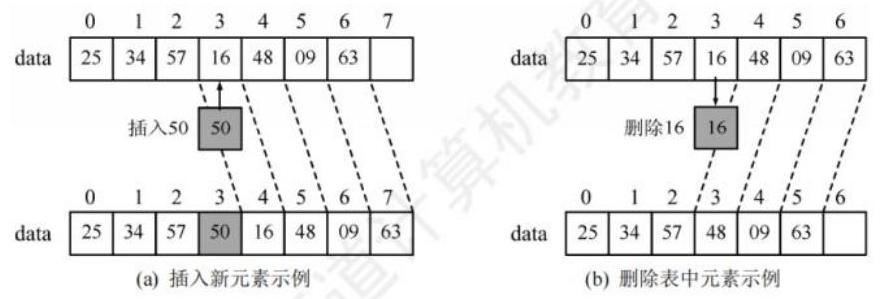
图 2.2 顺序表的插入和删除
4. 按值查找 (顺序查找)
在顺序表 L 中查找第一个元素值等于 e 的元素,并返回其位序。
int LocateElem(SqList L, ElemType e) {
for(int i = 0; i<L.length; i++) {
if(L.data[i] == e) {
return i+1; //下标为 i 的元素值等于 e ,返回其位序 i+1
}
}
return 0; //退出循环, 说明查找失败
}最好情况: 查找的元素就在表头,仅需比较一次,时间复杂度为
最坏情况: 查找的元素在表尾 (或不存在) 时,需要比较
平均情况: 假设 1<=i<=L.length+1 ) 个位置上的概率, 则在长度为
因此,顺序表按值查找算法的平均时间复杂度为
顺序表的按序号查找非常简单,即直接根据数组下标访问数组元素,其时间复杂度为
2.2.3 本节试题精选
一、单项选择题
13. 若长度为 n 的非空线性表采用顺序存储结构,在表的第 i 个位置插入一个数据元素,则 i 的合法值应该是 ( )。
A. 1≤i≤n B. 1≤i≤n+1 C. 0≤i≤n-1 D. 0≤i≤n
二、综合应用题
01. 从顺序表中删除具有最小值的元素 (假设唯一) 并由函数返回被删元素的值。空出的位置由最后一个元素填补,若顺序表为空,则显示出错信息并退出运行。
02. 设计一个高效算法,将顺序表 L 的所有元素逆置,要求算法的空间复杂度为
03. 对长度为 n 的顺序表 L ,编写一个时间复杂度为
04. 从顺序表中删除其值在给定值
05. 从有序顺序表中删除所有其值重复的元素, 使表中所有元素的值均不同。
06. 将两个有序顺序表合并为一个新的有序顺序表, 并由函数返回结果顺序表。
07. 已知在一维数组
08. 线性表
09. 给定三个序列 A、B、C ,长度均为 n ,且均为无重复元素的递增序列,请设计一个时间上尽可能高效的算法,逐行输出同时存在于这三个序列中的所有元素。例如,数组
给出算法的基本设计思想。
根据设计思想,采用 C 或 C++ 语言描述算法,关键之处给出注释。
说明你的算法的时间复杂度和空间复杂度。
10. 【2010 统考真题】设将
给出算法的基本设计思想。
根据设计思想,采用 C 或 C++ 或 Java 语言描述算法,关键之处给出注释。
说明你所设计算法的时间复杂度和空间复杂度。
11.【2011 统考真题】一个长度为
给出算法的基本设计思想。
根据设计思想,采用 C 或 C++ 或 Java 语言描述算法,关键之处给出注释。
说明你所设计算法的时间复杂度和空间复杂度。
12. 【2013 统考真题】已知一个整数序列
给出算法的基本设计思想。
根据设计思想,采用 C 或 C++ 或 Java 语言描述算法,关键之处给出注释。
说明你所设计算法的时间复杂度和空间复杂度。
13. 【2018 统考真题】给定一个含
给出算法的基本设计思想。
根据设计思想,采用 C 或 C++ 语言描述算法,关键之处给出注释。
说明你所设计算法的时间复杂度和空间复杂度。
14.【2020 统考真题】定义三元组
给出算法的基本设计思想。
根据设计思想,采用 C 或 C++ 语言描述算法,关键之处给出注释。
说明你所设计算法的时间复杂度和空间复杂度。
2.2.4 答案与解析
一、单项选择题
13. B
线性表元素的序号是从 1 开始,而在第 n+1 个位置插入相当于在表尾追加。
二、综合应用题
01. 算法思想: 搜索整个顺序表, 查找最小值元素并记住其位置, 搜索结束后用最后一个元素填补空出的原最小值元素的位置。
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MaxSize 100
#define ElemType int
typedef struct
{
ElemType data[MaxSize];
int length;
} SqList;
/**
* 从顺序表中删除最小元素
* @param L 指向顺序表的指针
* @param e 用于接收被删除最小元素的指针
* @return 删除是否成功
*
* 该函数首先检查顺序表是否为空,若为空则直接返回删除失败。
* 然后遍历顺序表找到最小元素及其索引,将最小元素值赋给e。
* 最后,用最后一个元素替换掉最小元素,并调整表长,完成删除操作。
*/
bool deleteMin(SqList *L, ElemType *e) {
/* 检查顺序表是否为空 */
if (L->length == 0) {
return false;
}
/* 初始化最小值及其索引 */
int min = L->data[0];
int minIndex = 0;
/* 遍历顺序表找到最小元素 */
for (int i = 1; i < L->length; i++) {
if (L->data[i] < min) {
min = L->data[i];
minIndex = i;
}
}
/* 将最小元素值赋给e */
*e = min;
/* 用最后一个元素替换掉最小元素 */
L->data[minIndex] = L->data[L->length - 1];
/* 调整顺序表长度 */
L->length--;
return true;
}
int main(int argc, char const *argv[])
{
SqList *L = (SqList *)malloc(sizeof(SqList));
L->data[0] = 0;
L->data[1] = 2;
L->data[2] = 2;
L->data[3] = 5;
L->data[4] = 5;
L->data[5] = 5;
L->data[6] = 9;
L->data[7] = 10;
L->length = 8;
ElemType e;
deleteMin(L, &e);
// 输出结果:10 2 2 5 5 5 9
for (int i = 0; i < L->length; i++)
{
printf("%d ", L->data[i]);
}
// 最小元素:0
printf("\n%d", e);
return 0;
}02 算法思想: 扫描顺序表 L 的前半部分元素,对于元素 L->data[i] (0 <=i<=L->length/2), 将其与后半部分的对应元素 L->data[L.length-i-1] 进行交换。
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MaxSize 100
#define ElemType int
typedef struct
{
ElemType data[MaxSize];
int length;
} SqList;
/*
* 函数名称:Reverse
* 函数功能:反转顺序表
* 参数列表:
* - L: 顺序表的指针,指向包含数据元素的数组和数组长度的结构体
* 返回值:无
*
* 函数实现的原理是通过交换数组中对称位置的元素来实现顺序表的反转。
* 例如,对于长度为n的顺序表,交换第i个元素和第n-1-i个元素,直到i等于n/2,即遍历完表的前半部分。
* 这样,原顺序表的前半部分就变成了新顺序表的后半部分,原顺序表的后半部分就变成了新顺序表的前半部分,
* 从而实现了顺序表的反转。
*/
void Reverse(SqList *L)
{
/* 从数组的开始和结束位置同时向中间遍历,直到遍历完数组的前半部分 */
for (int i = 0; i < L->length / 2; i++)
{
/* 交换对称位置的元素 */
ElemType temp = L->data[i];
L->data[i] = L->data[L->length - 1 - i];
L->data[L->length - 1 - i] = temp;
}
}
int main(int argc, char const *argv[])
{
SqList *L = (SqList *)malloc(sizeof(SqList));
L->data[0] = 0;
L->data[1] = 2;
L->data[2] = 2;
L->data[3] = 5;
L->data[4] = 5;
L->data[5] = 5;
L->data[6] = 9;
L->data[7] = 10;
L->length = 8;
Reverse(L);
// 输出结果:10 9 5 5 5 2 2 0
for (int i = 0; i < L->length; i++)
{
printf("%d ", L->data[i]);
}
return 0;
}03. 解法 1: 用 k 记录顺序表 L 中不等于 x 的元素个数 (即需要保存的元素个数),扫描时将不等于 x 的元素移动到下标 k 的位置,并更新 k 值。扫描结束后修改 L 的长度。 本题代码如下:
/*
* 删除顺序表中所有值为x的元素
* 参数 L: 顺序表的指针
* 参数 x: 需要删除的元素值
* 说明: 该函数通过遍历顺序表,将不等于x的元素重新排列到表的前面,然后调整表的长度,从而实现删除所有x的目的。
*/
void DeleteX(SqList *L, ElemType x)
{
/* k用于记录当前有效元素的个数 */
int k = 0;
/* 遍历顺序表中的每个元素 */
for (int i = 0; i < L->length; i++)
{
/* 如果当前元素不等于x,则将其移动到结果表的相应位置 */
if (L->data[i] != x)
{
L->data[k] = L->data[i];
k++;
}
}
/* 调整顺序表的长度,去除所有值为x的元素 */
L->length = k;
}解法 2: 用 k 记录顺序表 L 中等于 x 的元素个数,一边扫描 L ,一边统计 k ,并将不等于 x 的元素前移 k 个位置。扫描结束后修改 L 的长度。
/*
* 删除顺序表中所有值为x的元素,元素向左移动以填补空位。
* 参数 L: 顺序表的指针。
* 参数 x: 需要删除的元素值。
*/
void DeleteX2(SqList *L, ElemType x)
{
/* k用于记录待删除元素的总数,以便后续调整数组长度 */
int k = 0;
/* 遍历顺序表,查找并删除值为x的元素 */
for (int i = 0; i < L->length; i++)
{
/* 当前元素等于x时,k加一,表示找到一个待删除的元素 */
if (L->data[i] == x) {
k++;
} else {
/* 当前元素不等于x时,将元素向左移动以填补空位 */
/* 注意:这里不需要对k进行操作,因为只有在元素不等于x时才执行移动 */
L->data[i-k] = L->data[i];
}
}
/* 调整顺序表的长度,去除已删除的元素 */
L->length -= k;
}04. 解法1: 遍历顺序表,将不在给定范围内的元素保留至数组的前部,并更新顺序表的长度。
bool DeleteRange(SqList *L, ElemType s, ElemType t)
{
/* 检查顺序表是否为空 */
if (L->length == 0)
{
printf("顺序表为空\n");
return false;
}
/* 检查给定值s和t是否合理 */
if (s >= t)
{
printf("s >= t\n");
return false;
}
/* k用于记录当前有效元素的索引位置 */
int k = 0;
/* 遍历顺序表,*/
for (int i = 0; i < L->length; i++)
{
// 将不在范围[s, t]内的元素保留至数组的前部
if (L->data[i] < s || L->data[i] > t)
{
// 将当前元素移动到结果表的相应位置
L->data[k] = L->data[i];
/* k加一,表示找到一个待删除的元素 */
k++;
}
}
/* 更新顺序表的长度 */
L->length = k;
return true;
}解法2:从前向后扫描顺序表 L ,用 k 记录值在 s 和 t 之间的元素个数 (初始时 k = 0 )。对于当前扫描的元素,若其值不在 s 和 t 之间,则前移 k 个位置; 否则执行 k++ 。由于每个不在 s 和 t 之间的元素仅移动一次,因此算法效率高。
bool DeleteRange2(SqList *L, ElemType s, ElemType t)
{
/* 检查顺序表是否为空 */
if (L->length == 0)
{
printf("顺序表为空\n");
return false;
}
/* 检查给定值s和t是否合理 */
if (s >= t)
{
printf("s >= t\n");
return false;
}
/* k用于记录待删除元素的总数,以便后续调整数组长度 */
int k = 0;
for (int i = 0; i < L->length; i++)
{
/* 当前元素大于等于s且小于等于t时,表示找到一个待删除的元素 */
if (L->data[i] >= s && L->data[i] <= t)
{
k++;
}
else
{
/* 当前元素小于s或大于t时,将元素向左移动以填补空位 */
/*注意:这里不需要对k进行操作,因为只有在元素小于s或大于*/
L->data[i - k] = L->data[i];
}
}
L->length -= k;
return true;
}05. 算法思想: 注意是有序顺序表, 值相同的元素一定在连续的位置上, 用类似于直接插入排序的思想, 初始时将第一个元素视为非重复的有序表。之后依次判断后面的元素是否与前面非重复有序表的最后一个元素相同, 若相同, 则继续向后判断, 若不同, 则插入前面的非重复有序表的最后, 直至判断到表尾为止。
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MaxSize 100
typedef struct
{
int data[MaxSize];
int length;
} SqList;
/**
* 删除顺序表中的重复元素
* @param L 顺序表的指针
* @return 如果成功删除重复元素则返回true,否则返回false(即表为空)
*
* 该函数通过遍历顺序表,将不重复的元素重新排列在表的前部,然后调整表的长度,
* 从而实现删除重复元素的目的。重复元素的定义是值完全相同的元素。
*/
bool DeleteDupli(SqList *L)
{
/* 如果顺序表为空,则无需进行删除操作 */
if (L->length == 0)
{
return false;
}
/* i用于记录不重复元素的索引位置 */
int i = 0;
/* 从第二个元素开始遍历,比较当前元素与前一元素是否相同 */
for (int j = 1; j < L->length; j++)
{
/* 如果当前元素与前一元素不同,则将其移到结果序列的下一个位置 */
if (L->data[i] != L->data[j])
{
i++;
L->data[i] = L->data[j];
}
}
/* 调整顺序表的长度,去除后面的重复元素 */
L->length = i + 1;
/* 操作成功,返回true */
return true;
}
int main(int argc, char const *argv[])
{
SqList *L = (SqList *)malloc(sizeof(SqList));
L->data[0] = 0;
L->data[1] = 2;
L->data[2] = 2;
L->data[3] = 5;
L->data[4] = 5;
L->data[5] = 5;
L->data[6] = 9;
L->data[7] = 10;
L->length = 8;
DeleteDupli(L);
// 打印结果为 0 2 5 9 10
for (int i = 0; i < L->length; i++)
{
printf("%d ", L->data[i]);
}
return 0;
}06. 算法思想: 首先, 按顺序不断取下两个顺序表表头较小的结点存入新的顺序表中。然后, 看哪个表还有剩余, 将剩下的部分加到新的顺序表后面。
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
/** 静态分配的顺序表存储结构 */
#define MaxSize 100
#define ElemType int
typedef struct
{
ElemType data[MaxSize];
int length;
} SqList;
/** 动态分配的顺序表存储结构 */
#define InitSize 100 // 表长度的初始定义
typedef struct
{
ElemType *data; // 指示动态分配数组的指针
int maxSize, length; // 数组的最大容量和当前个数
} SeqList; // 动态分配数组顺序表的类型定义
// 合并两个有序表A和B到C
/**
* 合并两个有序顺序表
* @param A 第一个有序顺序表
* @param B 第二个有序顺序表
* @param C 指向用于存储合并结果的顺序表的指针
* @return 如果合并成功,则返回true;如果合并后的长度超过了C的最大大小,则返回false。
*
* 该函数将两个有序顺序表A和B合并到顺序表C中,并保持合并后的表也是有序的。
* 合并前,需要检查合并后的长度是否超过C的最大大小,以避免溢出。
* 合并过程中,通过比较A和B中的元素,将较小的元素依次放入C中,直到遍历完A或B中的所有元素。
* 最后,更新C的长度为合并后的长度。
*/
bool Merge(SeqList A, SeqList B, SeqList *C)
{
/* 检查合并后的长度是否超过C的最大大小 */
if (A.length + B.length > C->maxSize)
{
return false;
}
/* 初始化三个指针,分别指向A、B和C中的当前元素位置 */
int i = 0, j = 0, k = 0;
/* 当A和B中都有元素时,比较并合并较小的元素 */
while (i < A.length && j < B.length)
{
if (A.data[i] < B.data[j])
{
C->data[k++] = A.data[i++];
}
else
{
C->data[k++] = B.data[j++];
}
}
/* 当A中还有剩余元素时,将A中的剩余元素加入到C中 */
while (i < A.length)
{
C->data[k++] = A.data[i++];
}
/* 当B中还有剩余元素时,将B中的剩余元素加入到C中 */
while (j < B.length)
{
C->data[k++] = B.data[j++];
}
/* 更新C的长度为合并后的长度 */
C->length = k;
return true;
}
int main(int argc, char const *argv[])
{
SqList *L = (SqList *)malloc(sizeof(SqList));
L->data[0] = 0;
L->data[1] = 2;
L->data[2] = 2;
L->data[3] = 5;
L->data[4] = 5;
L->data[5] = 5;
L->data[6] = 9;
L->data[7] = 10;
L->length = 8;
SeqList *B = (SeqList *)malloc(sizeof(SeqList));
B->data = (ElemType *)malloc(sizeof(ElemType) * InitSize);
B->maxSize = InitSize;
B->length = 0;
B->data[0] = 0;
B->data[1] = 2;
B->data[2] = 2;
B->data[3] = 5;
B->data[4] = 5;
B->data[5] = 5;
B->data[6] = 9;
B->data[7] = 10;
B->length = 8;
SeqList *A = (SeqList *)malloc(sizeof(SeqList));
A->data = (ElemType *)malloc(sizeof(ElemType) * InitSize);
A->maxSize = InitSize;
A->length = 0;
A->data[0] = 0;
A->data[1] = 1;
A->data[2] = 1;
A->data[3] = 53;
A->data[4] = 55;
A->data[5] = 58;
A->data[6] = 99;
A->data[7] = 108;
A->length = 8;
SeqList *C = (SeqList *)malloc(sizeof(SeqList));
C->data = (ElemType *)malloc(sizeof(ElemType) * InitSize);
C->maxSize = InitSize;
C->length = 0;
Merge(*A, *B, C);
// 输出结果:0 0 1 1 2 2 5 5 5 9 10 53 55 58 99 108
for (int i = 0; i < C->length; i++)
{
printf("%d ", C->data[i]);
}
return 0;
}07. 算法思想: 首先将数组
/**
* 反转数组中指定范围的元素。
*
* @param A 数组A,包含需要反转的元素。
* @param left 要反转的子数组的左边界。
* @param right 要反转的子数组的右边界。
* @param Arraysize 数组A的大小。
*/
void Reverse(int A[], int left, int right, int Arraysize)
{
/* 检查边界条件,避免越界反转 */
if (left > right || right > Arraysize)
{
return;
}
/* 计算子数组的中间位置 */
int middle = (left + right) / 2;
/* 反转子数组的左侧一半和右侧一半 */
for (int i = left; i < middle - left; i++)
{
int temp = A[left + i];
A[left + i] = A[right - i];
A[right - i] = temp;
}
}
/**
* 交换数组中两个子数组的位置。
*
* 该函数的目的是将数组A中的前n个元素和后m个元素交换位置。
* 它通过三次调用Reverse函数来实现这个目标:首先反转整个区间[0, m+n-1],
* 然后反转前半部分[0, n-1],最后反转后半部分[n, m+n-1]。
* 这样,原始的前n个元素和后m个元素就会交换位置。
*
* @param A 数组A,包含需要交换位置的元素。
* @param m 后半部分子数组的长度。
* @param n 前半部分子数组的长度。
* @param Arraysize 数组A的大小。
*/
void Exchange(int A[], int m, int n, int Arraysize)
{
/* 反转整个区间[m, n],为后续交换做准备 */
Reverse(A, 0, m + n - 1, Arraysize);
/* 反转前半部分[0, n],使得前n个元素处于正确的位置 */
Reverse(A, 0, n - 1, Arraysize);
/* 反转后半部分[n, m],完成交换 */
Reverse(A, n, m + n - 1, Arraysize);
}12. 摩尔投票算法(Moore's Voting Algorithm)是一种用于在给定的数组中找到多数元素(即出现次数超过数组长度一半的元素)的方法。这种算法由Robert S. Boyer和J Strother Moore在1981年提出,因其高效性和简洁性而广受欢迎。
不同候选人的票数相消之后,再检验剩下的候选人的票数是否超过一半。
算法步骤
初始化:设定一个候选元素(candidate)和一个计数器(count)。初始时,候选元素可以是数组中的任意一个元素,计数器设为0。
遍历数组:
- 如果计数器为0,则将当前元素设为候选元素,并将计数器设为1。
- 如果当前元素等于候选元素,则将计数器加1。(票数加一)
- 如果当前元素不等于候选元素,则将计数器减1。(票数相消)
验证候选元素:经过遍历后,候选元素即为可能的多数元素。需要再遍历一次数组以验证该候选元素是否确实为多数元素。
时间复杂度
- 时间复杂度:O(n),因为数组被遍历了两次,每次遍历的时间复杂度为O(n)。
- 空间复杂度:O(1),因为只使用了常数个额外的空间。
示例
假设有一个数组
[1, 2, 3, 2, 2, 2, 5, 2],我们来一步步执行摩尔投票算法:- 初始状态:candidate = None, count = 0
- 遍历数组:
- 元素1:candidate = 1, count = 1
- 元素2:candidate = 1, count = 0(因为2 != 1)
- 元素3:candidate = 3, count = 1(因为count为0,更新candidate)
- 元素2:candidate = 3, count = 0(因为2 != 3)
- 元素2:candidate = 2, count = 1(因为count为0,更新candidate)
- 元素2:candidate = 2, count = 2
- 元素5:candidate = 2, count = 1(因为5 != 2)
- 元素2:candidate = 2, count = 2
经过第一次遍历,候选元素为2。接下来需要验证2是否为多数元素:
3. 验证阶段:遍历数组,统计候选元素2的出现次数,发现2出现了5次(大于数组长度的一半4次),因此2是多数元素。代码实现
以下是用Python实现摩尔投票算法的代码示例:
def majority_element(nums):
candidate = None
count = 0
# 第一遍遍历,找出候选元素
for num in nums:
if count == 0:
candidate = num
if num == candidate:
count += 1
else:
count -= 1
# 第二遍遍历,验证候选元素
count = 0
for num in nums:
if num == candidate:
count += 1
if count > len(nums) // 2:
return candidate
else:
return None
# 测试示例
nums = [1, 2, 3, 2, 2, 2, 5, 2]
print(majority_element(nums)) # 输出 2摩尔投票算法简洁高效,特别适用于寻找多数元素的问题。
下面是C的实现:
#include <stdio.h>
// 函数声明
int findCandidate(int* nums, int size);
int isMajority(int* nums, int size, int candidate);
// 主函数
int main() {
int nums[] = {1, 2, 3, 2, 2, 2, 5, 2};
int size = sizeof(nums) / sizeof(nums[0]);
int candidate = findCandidate(nums, size);
if (isMajority(nums, size, candidate)) {
printf("Majority element is %d\n", candidate);
} else {
printf("No majority element found\n");
}
return 0;
}
// 找出候选元素
int findCandidate(int* nums, int size) {
int candidate = 0;
int count = 0;
for (int i = 0; i < size; i++) {
if (count == 0) {
candidate = nums[i];
count = 1;
} else if (nums[i] == candidate) {
count++;
} else {
count--;
}
}
return candidate;
}
// 验证候选元素是否为多数元素
int isMajority(int* nums, int size, int candidate) {
int count = 0;
for (int i = 0; i < size; i++) {
if (nums[i] == candidate) {
count++;
}
}
return count > size / 2;
}13.
算法的基本设计思想:
要求在时间上尽可能高效,因此采用空间换时间的办法。分配一个用于标记的数组 B[n] ,用来记录 A 中是否出现了 B[0] 对应正整数 1, B[n-1] 对应正整数 B 中全部为 0 。由于 A 中含有 A 中 A 中出现了小于或等于 0 或大于 A 中出现了小于或等于 0 或大于
经过以上分析可以得出算法流程: 从 A[0] 开始遍历 A ,若 0<A[i]<=n,则令 B[A[i] - 1] = 1 ; 否则不做操作。对 A 遍历结束后,开始遍历数组 B ,若能查找到第一个满足 B[i] == 0 的下标 i , 返回 i + 1 即为结果,此时说明 A 中未出现的最小正整数在 1 和 n 之间。若 B[i] 全部不为 0,返回 i + 1 (跳出循环时 i = n , i + 1 等于 n + 1 ),此时说明 A 中未出现的最小正整数是 n + 1 。
算法实现:
/**
* 寻找缺失的最小正整数
* @param A 整数数组,其中可能包含正整数、负整数和零
* @param n 数组A的长度
* @return 返回缺失的最小正整数
*
* 该函数通过遍历数组A,将其中大于0且不超过n的整数对应位置的B数组元素标记为1。
* 随后再次遍历B数组,找到第一个值为0的元素位置,其索引+1即为缺失的最小正整数。
*/
int findMissMin(int A[], int n)
{
int i;
/* 分配与数组A长度相同的内存空间给B数组 */
int *B = (int *)malloc(sizeof(int) * n);
/* 初始化B数组所有元素为0 */
memset(B, 0, sizeof(int) * n);
/* 遍历数组A,将符合条件的元素在B数组中进行标记 */
for (i = 0; i < n; i++)
{
if (A[i] > 0 && A[i] <= n)
{
B[A[i] - 1] = 1;
}
}
/* 遍历B数组,寻找第一个未被标记的位置,即缺失的最小正整数 */
for (i = 0; i < n; i++)
{
if (B[i] == 0)
{
break;
}
}
/* 返回缺失的最小正整数 */
return i + 1;
}时间复杂度:
遍历 A 一次,遍历 B 一次,两次循环内操作步骤为 B[n] ,空间复杂度为